优化问题笔记
南京邮电大学课程:最优化方法——张伯雷
前言
本系列笔记的图片部分来自张伯雷老师的课堂ppt和网上,笔记仅供本人和需要的人学习使用。
优化问题介绍
优化问题1
题目
- 还有⼀个星期就要到期末考试,小明⼀共要考4门课,但只能复习70个小时,假设\(x=(x_1,x_2,...,x_4)\)代表小明分别花在4门课上的时间
- \(f_i(x)\), 𝑖 = 1, 2, 3, 4 为小明在第𝑖门课中的成绩
问题建模
最大化最终的总分数:\(\sum_if_i(x)\)
每门课都需要及格,同时花的时间不能超过70:
\(\sum_ix_i ≤ 70\), \(x_i ≥ 0\), \(f_i(x_i) ≥ 60\)
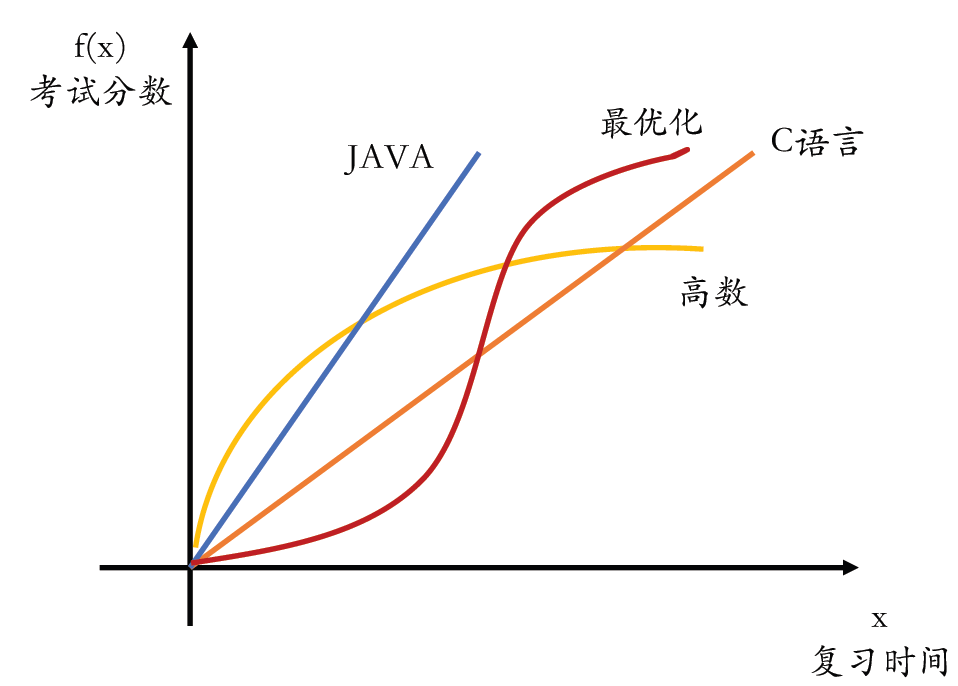
如何合理分配资源?
优化问题2
题目
- 小李是⼀个程序员,需要实现⼀个数据中⼼服务,当有用户请求服务时,需要尽快地服务用户请求,来降低整体延迟
- \(d_i(x_i)=1,2,...,n\)
- \(x_i\)为向用户𝑖分配的资源(如CPU的配额), \(d_i\)为第𝑖个用户的延迟
问题建模
最小化整体的延迟:\(\sum_id_i(x_i)\)
同时不能超过服务器的总资源:\(\sum_ix_i\le C\), \(x_i\ge0\)
如何合理分配资源?
优化问题3
题目
- 现在有⼀百万张图片,⼀共分成了1000个类别𝑝,我们设计了⼀个复杂的神经⽹络,可以输入图片矩阵输出类别概率𝑞。为了训练这个神经⽹络,需要优化该网络,最小化预测误差。
问题建模
\[ min-\sum_{x\in X} p(x)\log q(x) \]
神经网络可能包括上亿的参数,如何快速优化?
优化/数学规划
优化问题
\[ \min f_0(x).\\ \text{s.t.}\ \ f_i(x)\le0,\quad i=1,...,m \]
其中
- \(x=(x_1,x_2,...,x_n)\):优化变量(variable)
- \(f_0: \mathbb{R}^n\rightarrow\mathbb{R}\):目标函数(Objective function)
- \(f_i: \mathbb{R}^n\rightarrow\mathbb{R},i=1,...m\):约束函数(Constraints)
- 最优解\(x^*\):所有在定义域且满⾜约束条件的解中使得目标函数\(f_0\)最小的\(x\)
- 最优值\(p*:f_0(x^*)\)
优化问题分类
线性/非线性规划
线性规划:
- 如果目标函数与约束函数都是线性的,则为线性规划(Linear programming)
- \(f_i(\alpha x+\beta y)=\alpha f_i(x)+\beta f_i(y),i=0,1,...,m\)
- 单纯形法(simplex method)
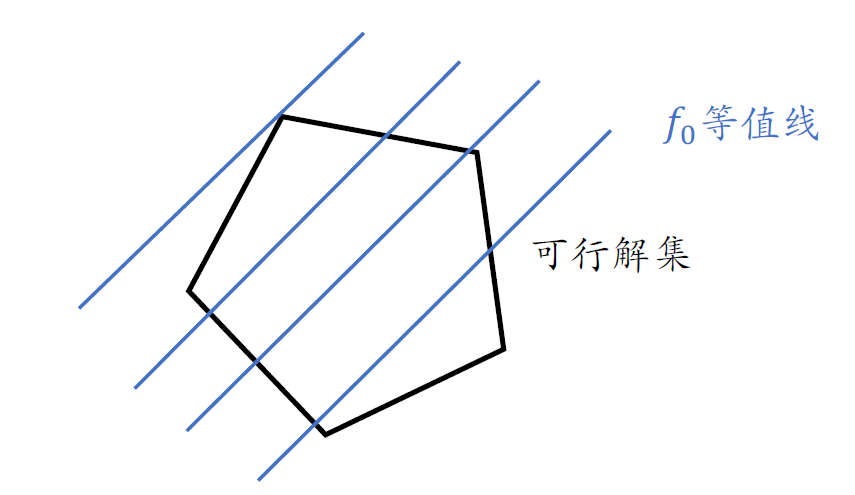
非线性规划:
- 如果目标函数与约束函数有⼀个不是线性的,则为非线性规划(Non-Linear programming)
凸/非凸规划
凸规划:
- 可行解集是凸集,目标函数是凸函数
- \(f_i(\alpha x+\beta y)\le\alpha f_i(x)+\beta f_i(y),i=0,1,...,m\)
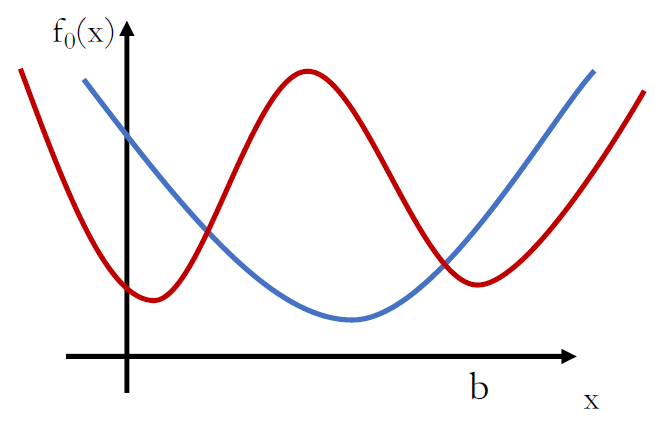
非凸规划:
- 可行解集不是凸集或目标函数不是凸函数
光滑/非光滑规划
光滑规划:
- 如果目标函数\(f_0(x)\)是光滑的
- 光滑:在函数的每⼀点都可微
非光滑规划
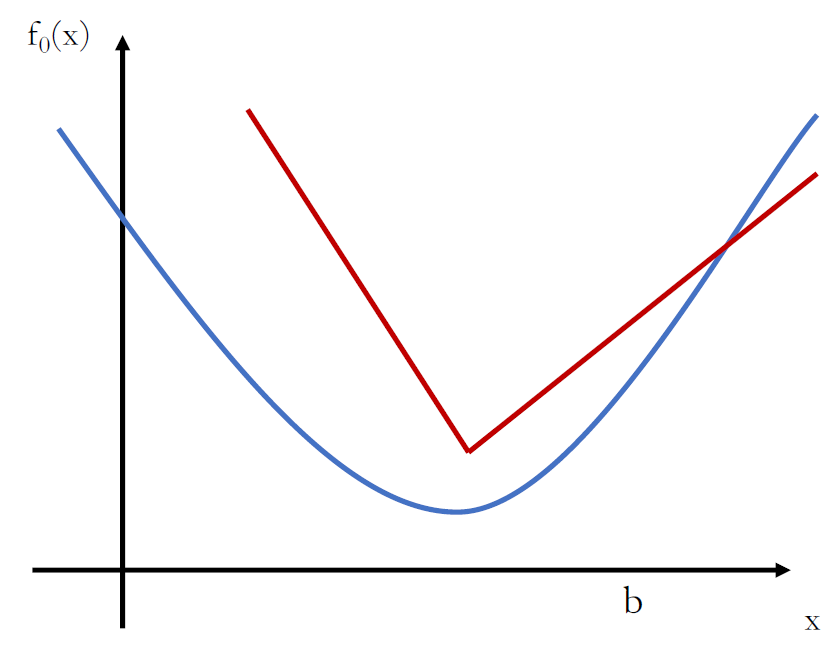
连续/离散规划
连续规划:
- 可行解集是⼀个连续的域
离散规划:
- 可行解集是离散的
单目标/多目标规划
多目标规划:
- 同时有多个需要优化的目标
- \(\min f_1(x),f_2(x)\)
- 可以通过加权转化为单目标优化问题

博弈优化

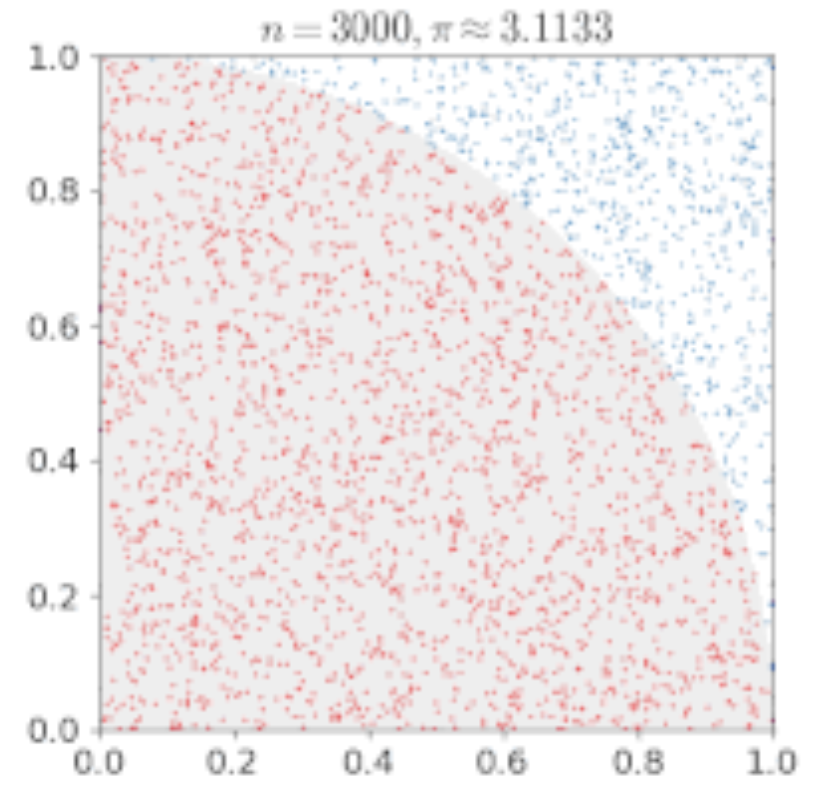
确定/随机优化
典型优化问题
最小二乘
数据拟合问题:
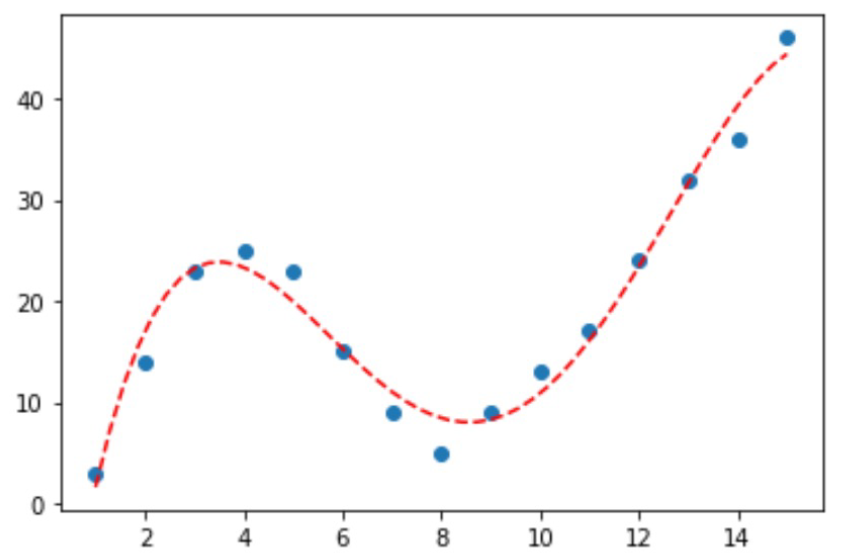
- 目标函数
\[ \min\sum^N_{i=1}\left(y_i-f(x_i)\right)^2 \]
稀疏优化
考虑线性方程组求解问题
\[ Ax=b \]
其中\(x\in R^n,b\in R^m,A\in R^{m\times n}\)
向量\(b\)的维度远小于向量\(x\)的维度,即\(m\ll n\)
- 在信号传输过程中,希望通过接收到长度为\(m\)的数字信号\(b\)精确地重构原始信号\(x\)
- 方程组是欠定的,因此存在无穷多个解,重构出原始信号看似很难
稀疏先验:精确解\(u\)只有\(10\%\)的元素非零,即\(u\)是如下\(l_0\)范数问题的最优解:

- \(l_0\)范数优化问题是 NP 难问题
- 但\(l_1\)范数优化问题的解可以非常容易地通过现有优化算法得到
- 若\(A,b\)满足一定的条件,向量\(u\)也是\(l_1\)范数优化问题的唯⼀最优解
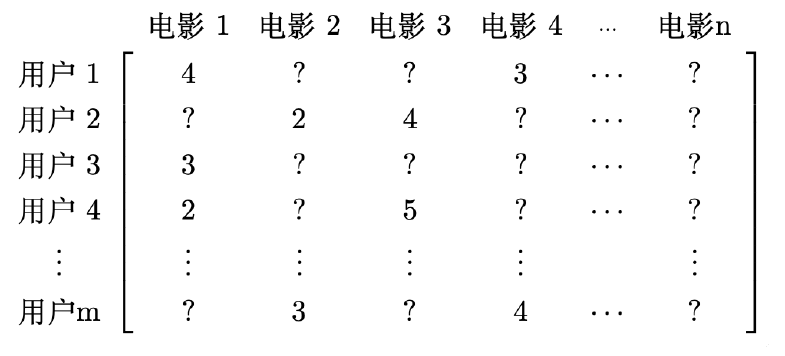
低秩矩阵恢复
- 某视频网站提供了约 48 万用户对 1 万 7 千多部电影的上亿条评级数据,希望对用户的电影评级进行预测,从而改进用户电影推荐系统,为每个用户更有针对性地推荐影片
- 用矩阵𝑀代表用户评分,每一行表示不同用户,每⼀列表示不同电影

深度学习
深度学习分类问题
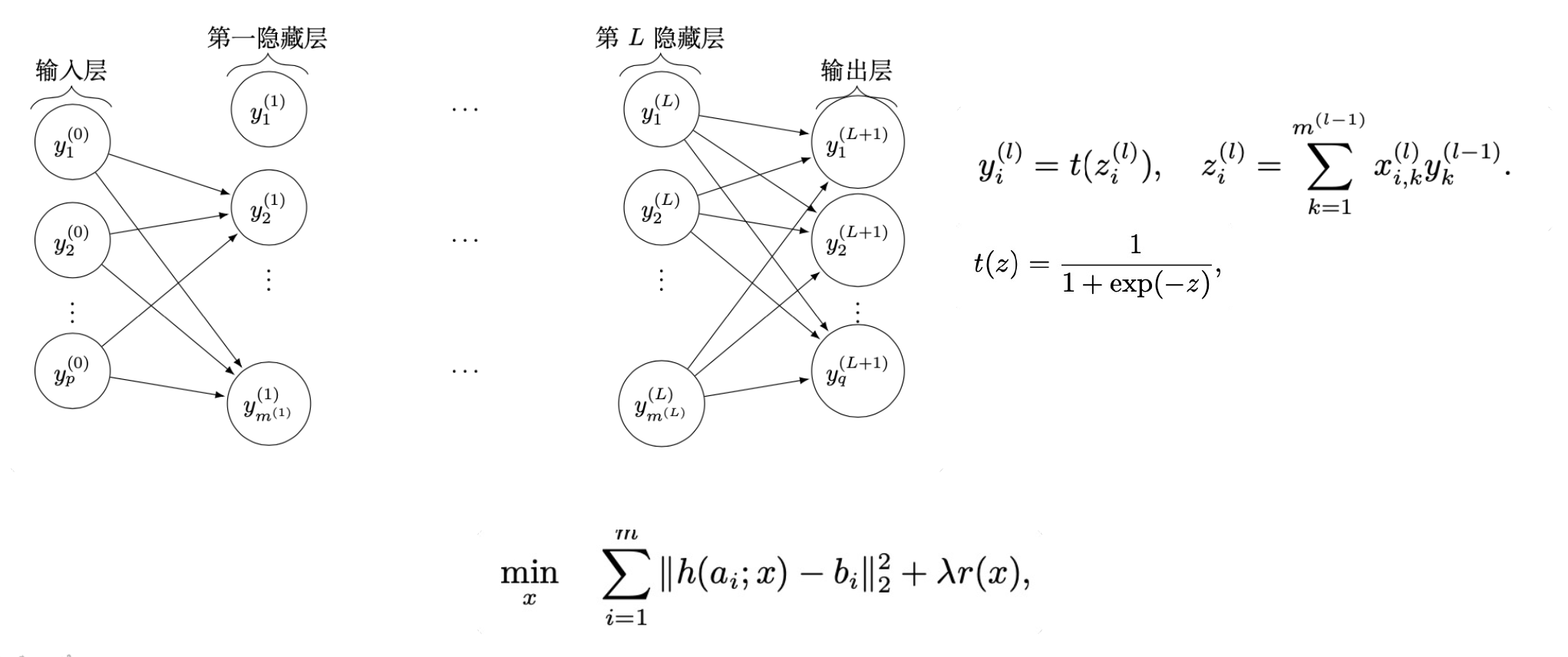
求解优化问题
对有限资源进⾏有效分配和控制,并达到某种意义上的最优。
通常需要 • 对需求进行定性和定量分析 • 建立恰当的数学模型来描述该问题 • 探索研究模型和算法的理论性质,考察算法的计算性能等 • 设计合适的计算方法来寻找问题的最优解
一般的最优化问题
- 非常难以求解
- 可能需要非常长的计算时间,甚⾄找不到最优解
⼀类相对简单的问题
- 最小二乘问题
- 线性规划问题
- 凸优化问题
更复杂的问题
- 离散、博弈、随机优化
定义域
- 凸集
目标函数
- 凸函数
非凸优化问题与凸优化问题的转化
- 等价转化
- 对偶理论
优化算法
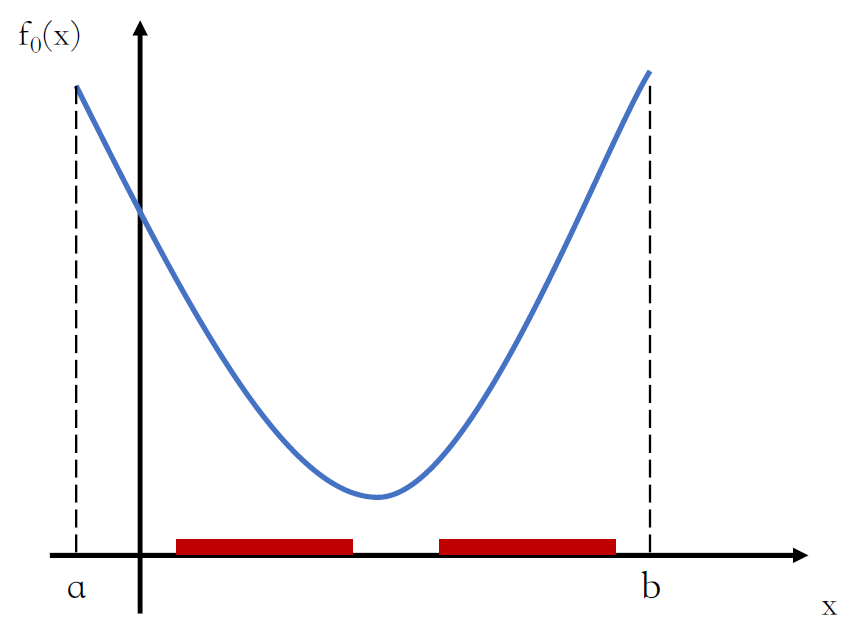
闭式解(closed form solution)
- 如果我们能用代数表达式给出其最优解,那么这个解称为闭式解,对应的问题往往比较简单
- 例如:⼆次函数在有界区间上
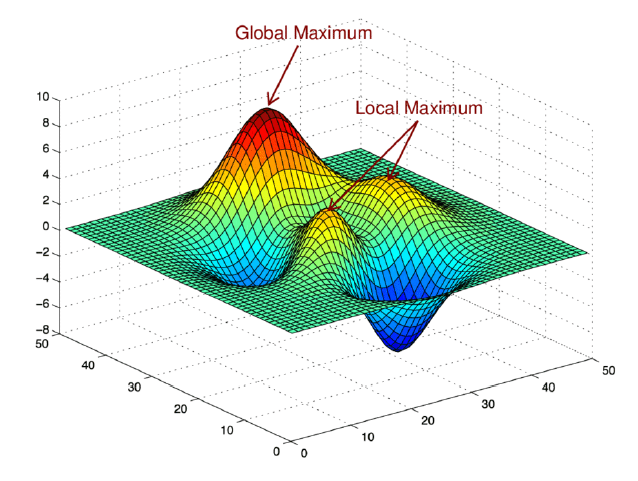
实际大多数问题是没有闭式解的,需要通过迭代算法求解
- 迭代算法的基本思想是:从⼀个初始点\(x_0\)出发,按照某种给定的规则进行迭代,得到⼀个序列\(\{x^k\}\)如果迭代在有限步内终止,那么希望最后一个点就是优化问题的解
- 例如:梯度类算法、线搜索法、罚函数法
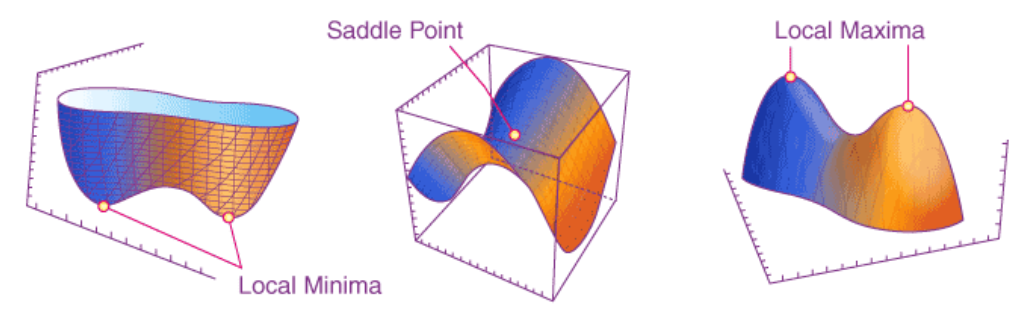
常用优化技巧
泰勒展开
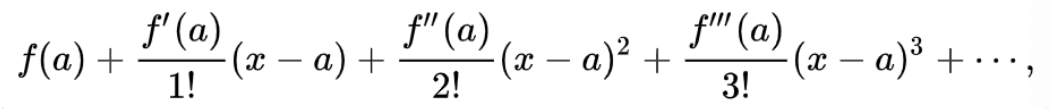
对偶
- 每个优化问题都有对应的对偶问题,特别是凸的情形,当原始问题比较难解的时候,其对偶问题可能很容易求解
拆分
- 通过引入变量等方法,讲⼀个复杂的优化问题拆分成多个相对简单的问题