凸集(Convex Set)
第二课:凸集(Convex Set)
重要定义
仿射集
直线:
对于穿过\(x_1,x_2\)两个不同的点的直线,所有满足以下条件的点:
\[
x=\theta x_1+(1-\theta)x_2,\theta\in\mathbb{R}
\]
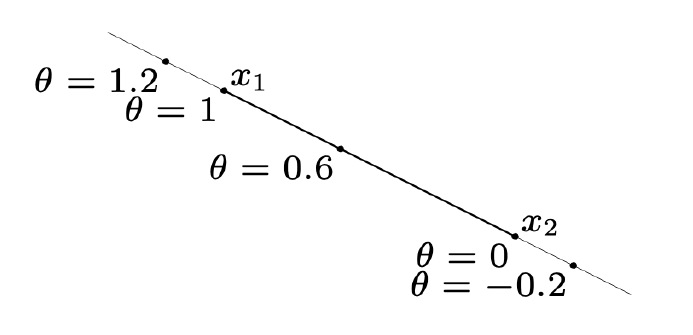
仿射集
一个集合\(C\)是仿射集,若\(\forall x_1,x_2\in C\),连接\(x_1,x_2\)的直线也在\(C\)内
思考:
- 该条直线上所有的点组成的集合(是)
- 空集、点、线段是仿射集吗?(空集是,点是,线段不是)
- 实数集、正实数集、整数集是仿射集吗?(实数集是、正实数集不是、整数集不是)
凸集(Convex Set)
线段:
对于穿过\(x_1,x_2\)两点的直线,所有满足以下条件的点: \[ x=\theta x_1+(1-\theta)x_2,0\le\theta\le1 \]
凸集:
集合中任意两点组成的线段仍在该集合中: \[ x_1,x_2\in C,0\le\theta\le1.\Rightarrow\theta x_1+(1-\theta)x_2\in C \] 例子:
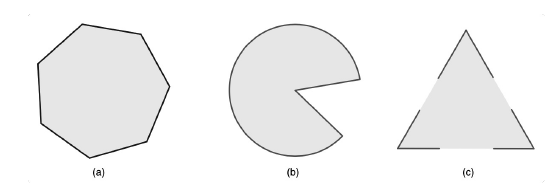
思考:
- 点、直线(点是,直线也是)
- 实数集、正实数集、整数集是否为凸集(都不是)
- 仿射集是否为凸集(是)
凸组合与凸包
凸组合(Convex Combination):
对于任意点k个点:\(x_1,x_2,...,x_k\),凸组合是以下的形式: \[ x=\theta_1 x_1+\theta_2 x_2+···\theta_k x_k \]
其中\(\theta_1+\theta_2+···+\theta_k=1,\theta_i\ge0\)
\(C\)为凸集\(\Leftrightarrow\)\(C\)中任意元素点凸组合属于\(C\)
凸包(Convex Hull):
\(conv C\):所有集合\(C\)中的点的凸组合,是包含\(S\)的最小的凸集
用一个绳子连起来:
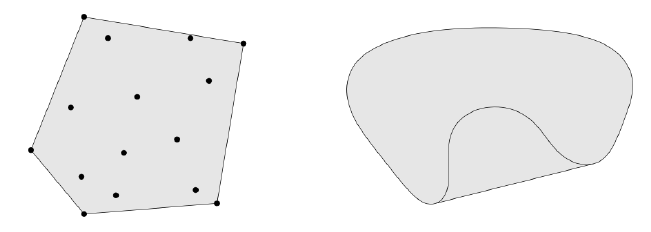
凸锥(Convex Cone)
锥:
\(C\)为锥\(\Leftrightarrow\)对于\(C\)中任意的点\(x\),\(\theta x\in C,\theta\ge0\)
凸锥:
对于任意的两个点:\(x_1,x_2\),凸锥是以下的形式: \[ x=\theta_1 x_1+\theta_2 x_2 \]
其中\(\theta_1\ge0,\theta_2\ge0\)
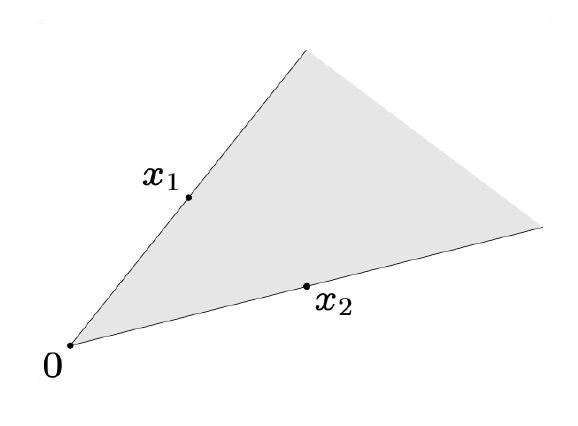
思考:
- 原点是否一定在凸锥上?(是)
- 经过原点的射线(是)
- 经过原点的直线(是)
- 凸锥是凸集吗?(是)
仿射集、凸集、凸锥的关系
定义:
- 仿射集:\(\theta_1+\theta_2=1\)
- 凸集:\(\theta_1+\theta_2=1,\theta_i\ge0\)
- 凸锥:\(\theta_i\ge0\)
关系:
- 仿射集\(\subseteq\)凸集
- 凸锥\(\subseteq\)凸集
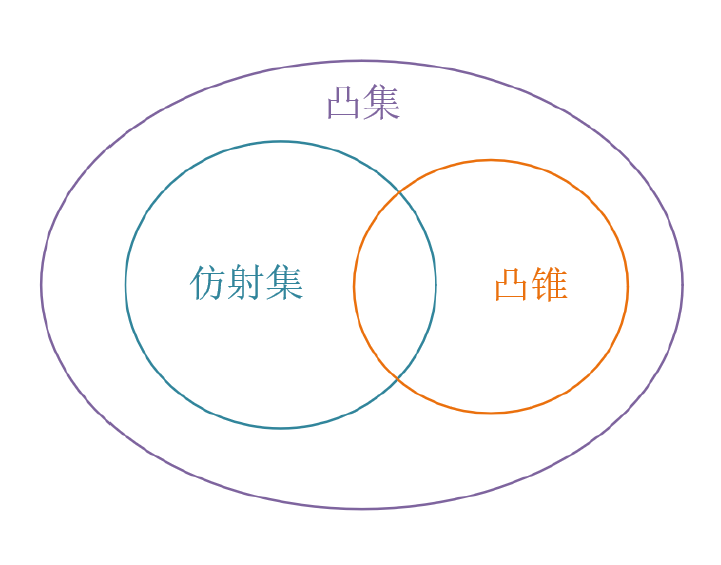
几种重要的凸集
超平面和半空间
超平面:
满足以下条件的点的集合: \[
\{x|a^T \boldsymbol{x}=b\}(a\neq0)
\]
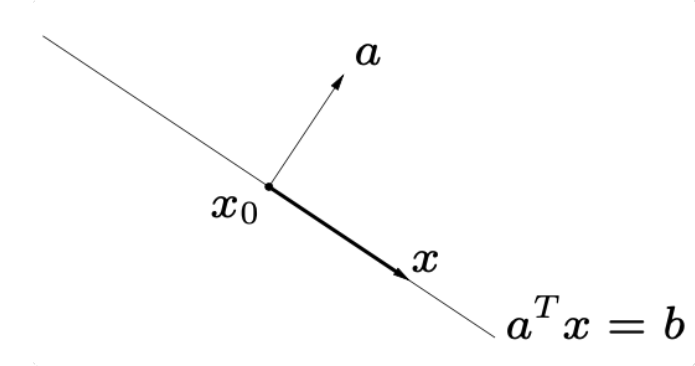
超平面是仿射的,也是凸的
半空间:
\[ \{x|a^T\boldsymbol{x}\le b(a\neq0)\} \]
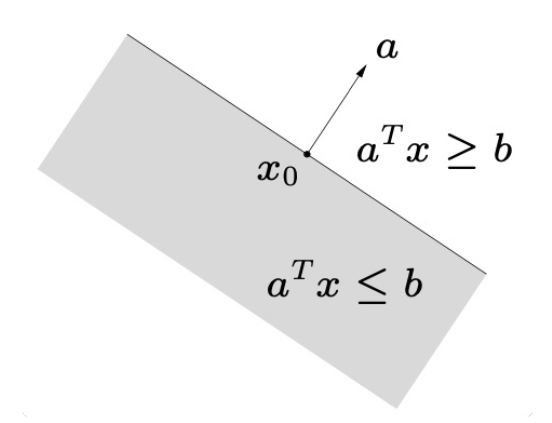
多面体
- \(\{x|Ax\le b,Cx=d\}\)
- \(A\in R^{m\times n},C\in R^{p\times n}\)
- 多面体是有限个半空间和超平面的交集
- 多面体是凸集
对称半正定矩阵
预备知识:
对称矩阵\(S^n\):
是指以主对角线为对称轴,各元素对应相等的矩阵 \[ \begin{bmatrix} a_{11}&a_{12}&a_{13}&···&a_{1n}\\ a_{21}&a_{22}&a_{23}&···&a_{2n}\\ a_{31}&a_{32}&a_{33}&···&a_{3n}\\ \vdots&\vdots&\vdots&\vdots&\vdots\\ a_{m1}&a_{m2}&a_{m3}&···&a_{mn} \end{bmatrix} \]
对称半正定矩阵:
给定一个大小为\(n\times n\)的实对称矩阵\(A\),若对于任意长度的\(n\)的非零向量\(x\),有\(x^TAx\ge0\)恒成立,则矩阵\(A\)是一个半 正定矩阵
堆成正定矩阵\(S^n_{++}\)
对称半正定矩阵集合:
\[ S^n_+=\{X\in S^n|X\succeq0\} \]
对称半正定矩阵集合是凸锥

球与椭球
球:
满足以下条件的点的集合: \[ B(x_c,r)=\{x|\|x-x_c\|_2\le r\}=\{x_c+ru|\|u\|_2\le1\} \]
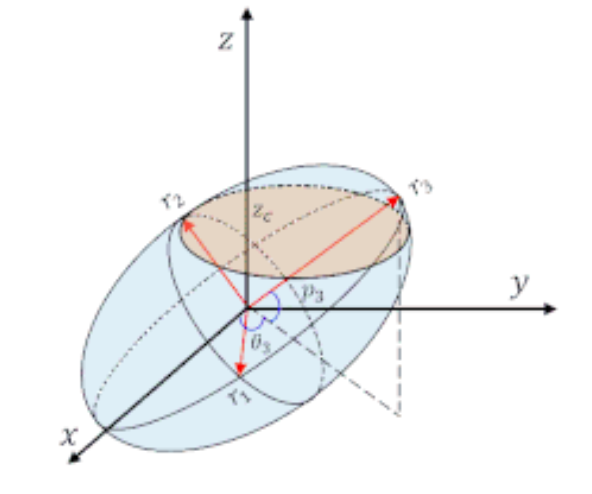
椭球:
\[ \{x|(x-x_c)^TP^{-1}(x-x_c)\le1\},P\in S^n_{++} \]
球是凸集
保凸的运算
交集
定理:任意多个凸集的交集为凸集
仿射变换
定理:设\(f:\mathbb{R}^n\rightarrow\mathbb{R}^m\)是仿射变换\((f(x)=Ax+b, A\in\mathbb{R}^{m\times n},b\in \mathbb{R}^m)\)则:
(1)凸集在\(f\)下的像是凸集: \[ S\subseteq\mathbb{R}^n是凸集\Rightarrow f(S)\overset{\text{def}}{=}\{f(x)|x\in S\}是凸集; \] (2)凸集在\(f\)下的原像是凸集: \[ C\subseteq\mathbb{R}^m\Rightarrow f^{-1}(C)\overset{\text{def}}{=}\{x\in\mathbb{R}^n|f(x)\in C\}是凸集. \]
缩放、平移和投影都是仿射变换
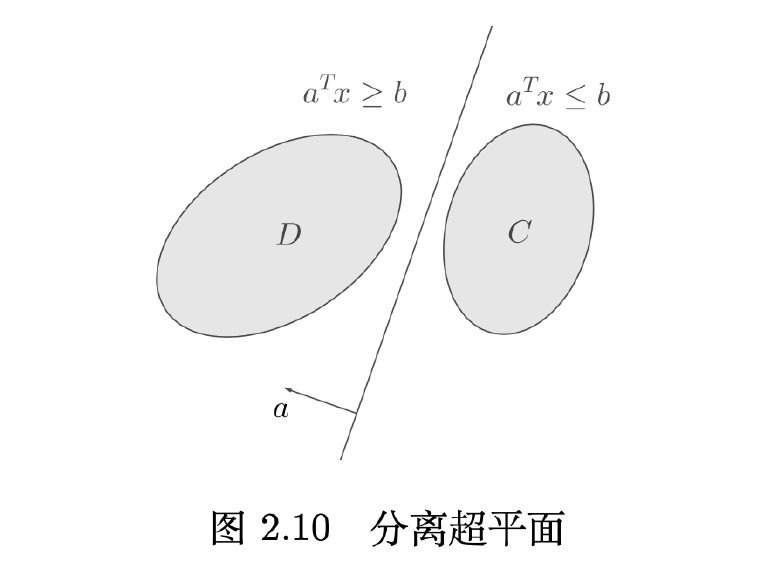
分离超平面定理
如果\(C\)和\(D\)是不相交的两个凸集,则存在非零向量\(a\)和常数\(b\),使得 \[
a^Tx\le b, \forall x\in C,且a^Tx\ge b,\forall x\in D,
\]
支撑超平面定理
