凸优化问题
凸优化问题
优化问题的标准形式
一般优化问题
优化问题
\[ \min f_0(x).\\ \text{s.t.}\ \ f_i(x)\le0,\quad i=1,...,m\\ h_i(x)=0,\quad i=1,..., \]
其中
- \(x=(x_1,x_2,...,x_n)\):优化变量(variable)
- \(f_0: \mathbb{R}^n\rightarrow\mathbb{R}\):目标函数(Objective function)
- \(f_i: \mathbb{R}^n\rightarrow\mathbb{R},i=1,...m\):不等式约束(Constraints)
- \(h_i: \mathbb{R}^n\rightarrow\mathbb{R},i=1,...p\):等式约束(Constraints)
- \(m=p=0:\)无约束问题
优化问题的最优解
优化问题的域(domain) \[ D=\bigcap_{i=0}^m domf_i\cap\bigcap_{i=1}^p domh_i \]
可行解集(feasible set) \[ 𝑋 = \{𝑥 ∈ 𝐷且所有约束条件可以满⾜\} \]
问题的最优值(optimal value) \[ p^* = \inf\{f_0(𝑥)|𝑥 ∈ 𝑋_f\} \]
最优解(optimal point/solution) \[ 若x^*可⾏,且f_0(x^*)=p^* \]
最优解集(optimal set) \[ x_{opt}=\{x|x\in X_f,f_0(x^*)=p^*\} \]
\(\varepsilon\)-次优解集( \(\varepsilon\)–suboptimal set) \[ X_\varepsilon=\{x|x\in X_f,f_0(x^*)\le p^*+\varepsilon\} \]
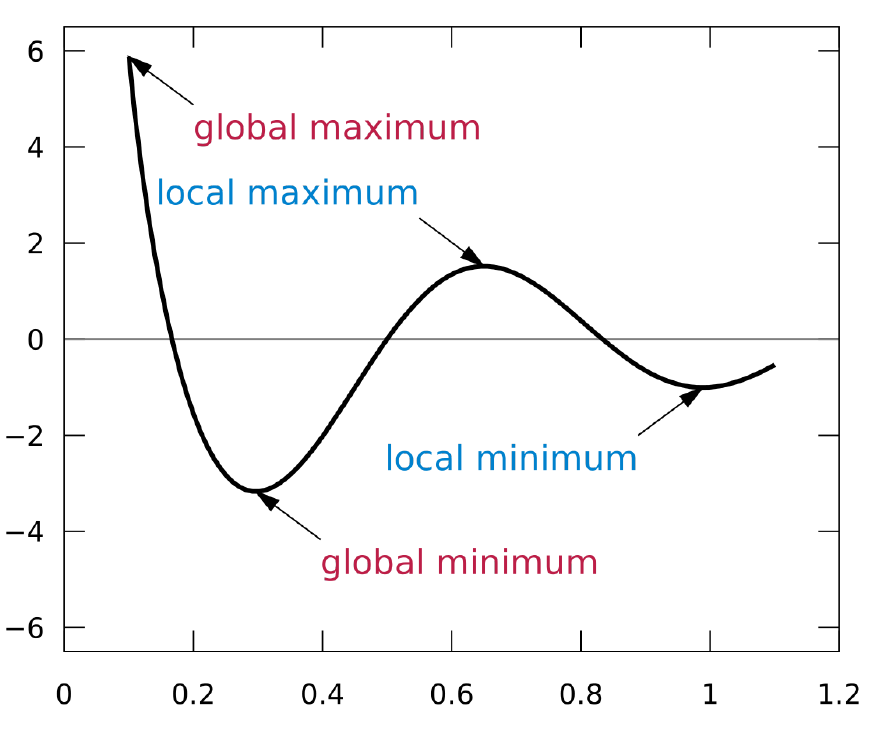
局部最优解(Locally optimal)
- 𝑥为局部最优解,如果\(\exist R>0\)使得\(x\)为以下问题的最优解:
- 所有局部最优解构成的解集为\(X_loc\)
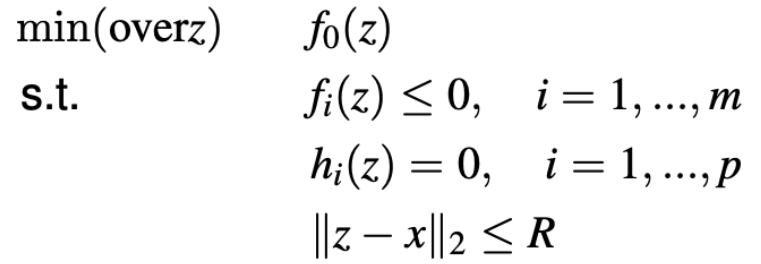
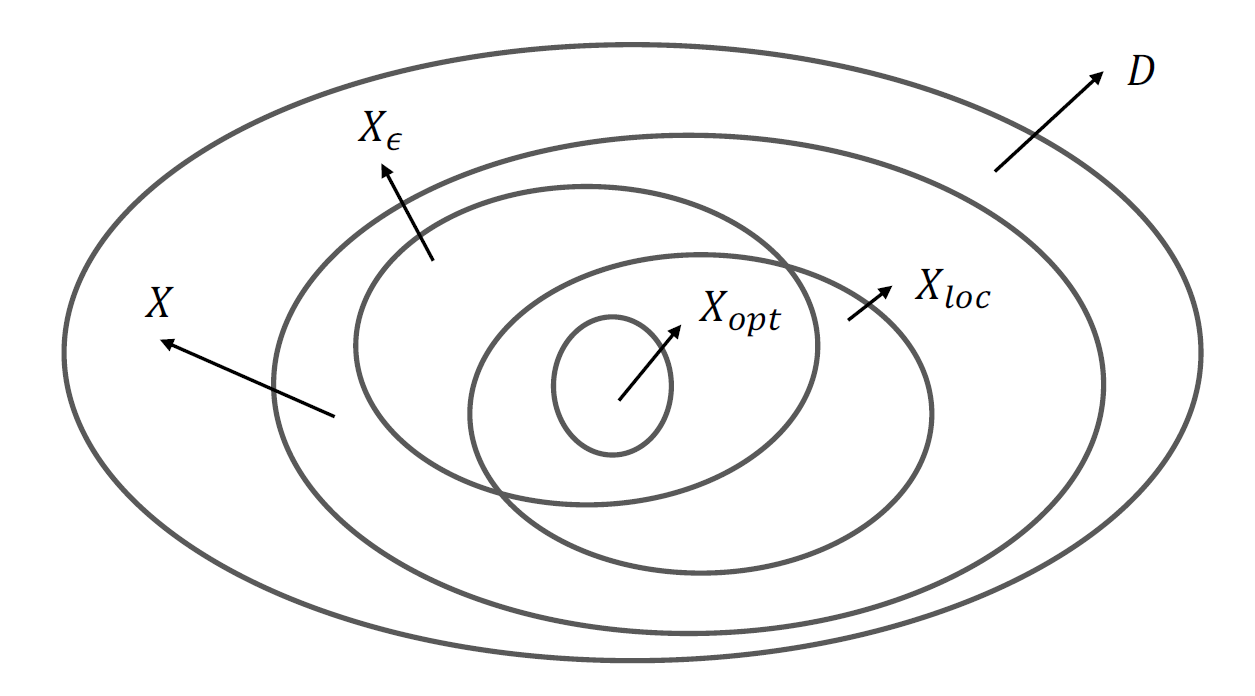
不同解集的关系
凸优化问题

例:
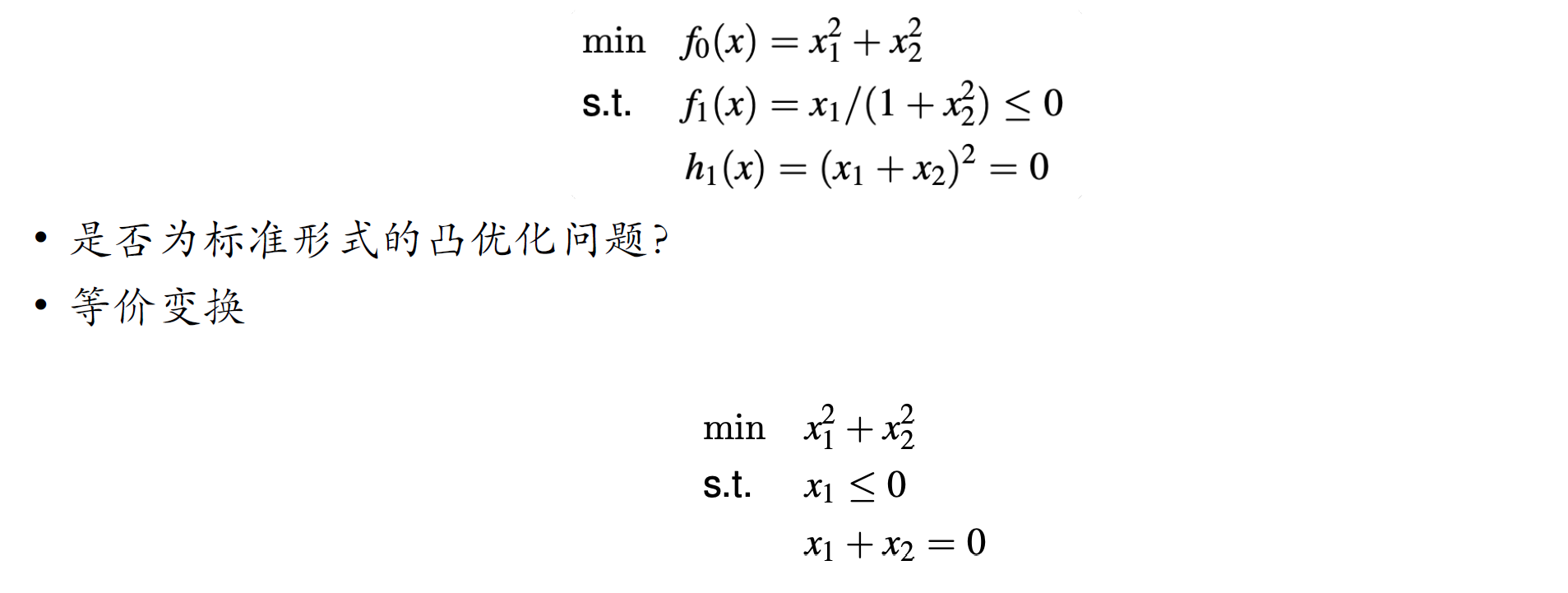

重要性质:局部最优=全部最优
局部最优=全部最优
局部最优:存在\(R>0\)使得\(x\)为以下问题的最优解: \[ \min(overz)\quad f_0(z)\\ \text{s.t.}\quad\quad f_i(z)\le0,\quad i =1,...,m\\ \quad \quad \quad h_i(z)=1,\quad i =1,...,p\\ \|z-x\|_2\le R \]
全局最优:\(p^*=\inf \{f_0(x)|x\in D_f\},\quad f_0(x^*)=p^*\)
最优条件
可微目标函数下的最优条件
凸函数的一阶条件
- \(f_0\)可微,则\(f_0\)为凸函数\(\Rightarrow domf\)为凸集
- \(f_0(y)\ge f_0(x)+\nabla f_0^T (x)(y-x), \forall x,y\in dom f\)
最优条件
- \(x\in X\)最优\(\Leftrightarrow \nabla f_0(x)^T (y-x)\ge0 \text{ for all }y\in X\)
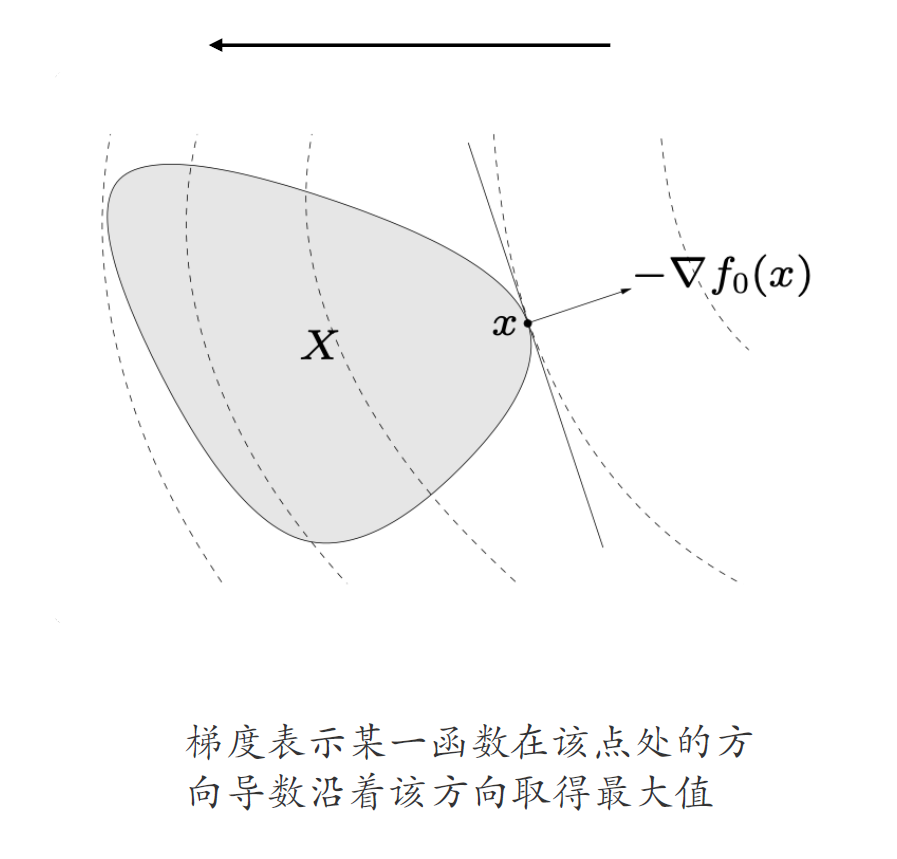
最优条件(特殊情况)
无约束问题:
\(x\)为最优解的充分必要条件 \[ x\in \text{dom}f_0,\quad \nabla f_0(x)=0 \]
等式约束问题:
\[ \min\quad f_0(x)\quad \text{s.t.}\quad Ax=b \]
\(x\)为最优解的充分必要条件。存在\(v\)使得 \[ x\in \text{dom}f_0,\quad Ax=b,\quad \nabla f_0(x)+A^Tv=0 \]
典型优化问题
线性规划(Linear Programming)
\[ {align*} \min\quad c^Tx+d\\ \text{s.t.}\quad Gx\le h\\ Ax=b \] {align*}

二次规划(Quadratic Programming)
\[ \min\quad (1/2)x^TPx+q^Tx+r\\ \text{s.t.}\quad Gx\le h\\ Ax=b \]
- \(P\in S^n_+\),凸优化问题
- 可行解时多面体,虚线为等高线
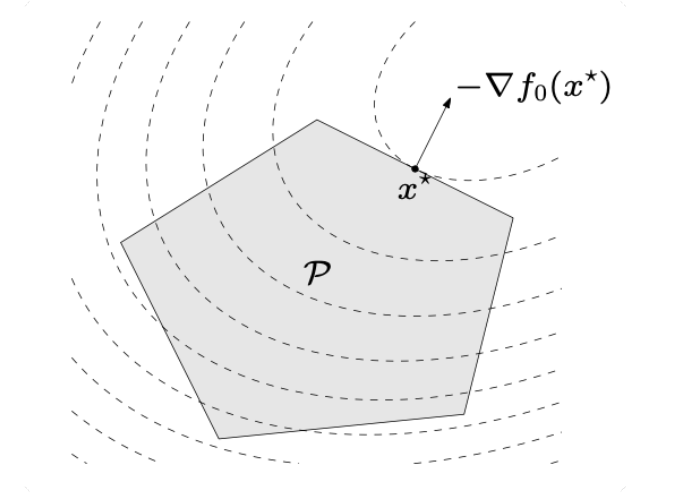
二次约束二次规划(QCQP)
\[ \min\quad (1/2)x^TP_0x+q_0^Tx+r_0\\ \text{s.t.}\quad (1/2)x^TP_ix+q_i^Tx+r_i\le0,\quad i=1,...,m\\ Ax=b \]
- \(P\in S^n_+\),目标函数与不等式约束都是二次凸函数
- 可行解集为m个椭球和⼀个仿射集的交集
例-最小二乘问题(Least Squares Problem)
\[ \min\|Xw-y\|^2_2\\ \min\quad w^TX^TXw-2y^TXw+y^Ty \]
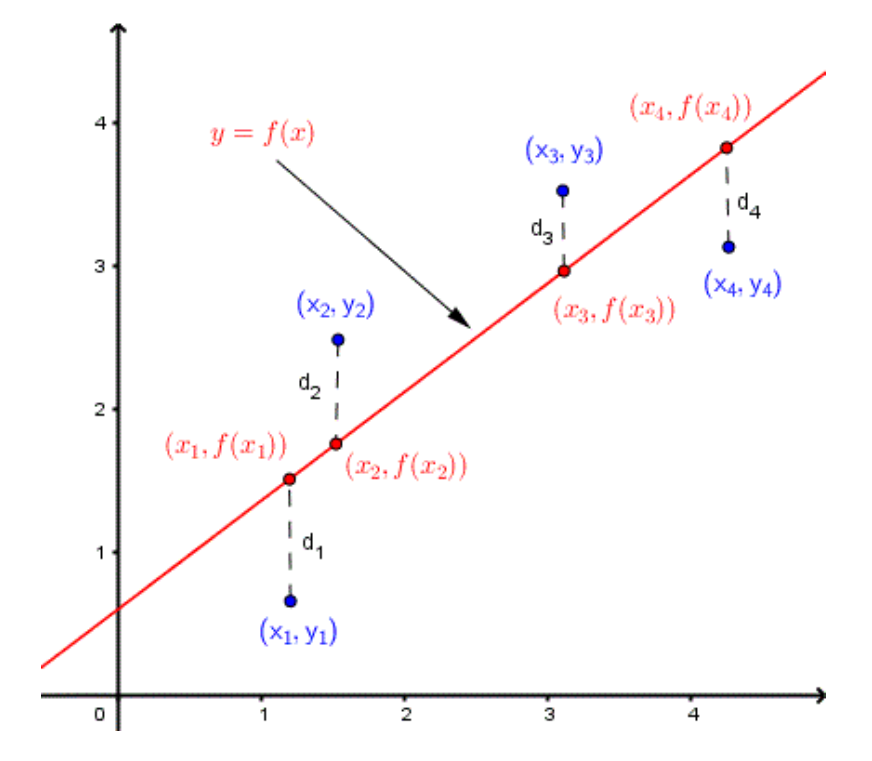
- 无约束QP问题
- 解析解:\((X^TX)^{-1}X^Ty\)
- 假设有约束\(u_i\le w_i\le l_i\),则是一个具有等式约束的QP问题
例-投资组合问题(portfolio problem)
\[ \begin{aligned} & \max \sum_{i=1}^n x_i p_i . \\ & \text { s.t. } \sum_{i=1}^n x_i \leq B, x_i \geq 0 \end{aligned} \]
其中\(x_i\)为第\(i\)种产品的投资额,\(B\)为总资金, \(p_i\)为收益率
- 在实际情况中, \(p_i\)⼀般为概率分布
- \(\bar{p}=[1.05, 1.05, 1]\)
- \(\sum =[1.2, 2, 0]\)
\[ \begin{array}{ll} \min & \sum_{i=1}^n X^T \sum X \\ \text { s.t. } & \bar{p}^T X \geq r_{\text {min }}, I^T X=B, X \geq 0 \end{array} \]
复合优化问题
\[ \min \psi (x)=f(x)+h(x) \]
其中,\(f(x)\)一般是凸的、光滑的,\(h(x)\)一般是凸的,但不一定光滑
应用场景:
- 岭回归:\(f(x)\)为最小二乘,\(h(x)=\|x\|_2\)
- Lasso:\(f(x)\)为最小二乘,\(h(x)=\|x\| _1\)
- l1范数正则化逻辑回归:\(f(x)=\sum_{i=1}^m \ln(1+\exp(-b_i\cdot a^T_i x)),h(x)=\|x\|_1\)
- l1范数正则化支持向量机:\(Cf(x)=\sum_{i=1}^m \max\{1+(-b_i(a^T_i x +y),0\},h(x)=\|x\|_1\)
l1正则化与l2正则化
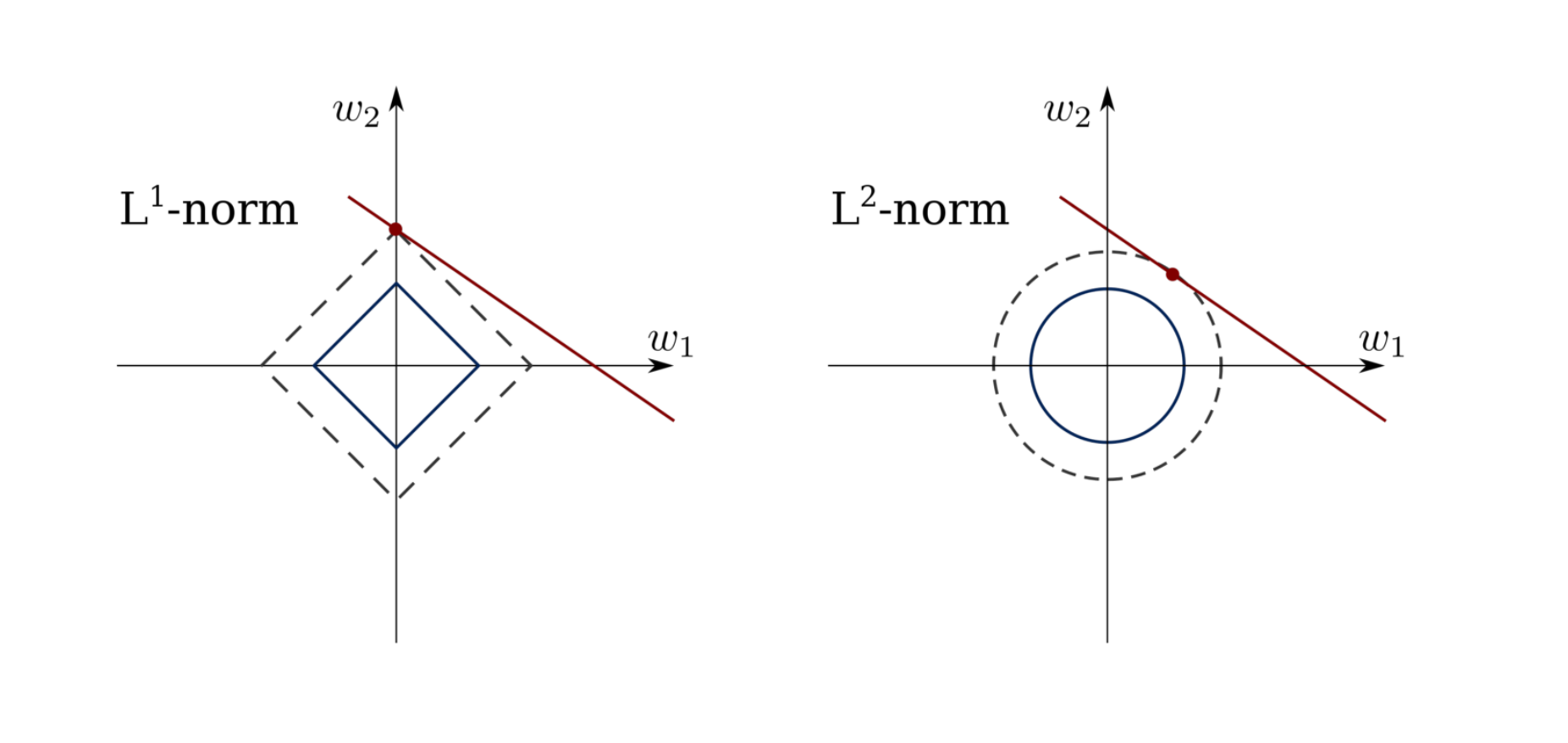
矩阵优化
\[ \min \quad\psi (x) \]
- \(X包含n\times n个元素\)
- 半定规划
\[ \begin{aligned} \min & c^{\mathrm{T}} x \\ \text { s.t. } & x_1 A_1+x_2 A_2+\cdots+x_n A_n+B \preceq 0 \\ & G x=h, \end{aligned} \]
例-低秩矩阵恢复

整数规划(非凸)
\[ \begin{array}{ll} \min & c^{\top} x \\ \text { s.t. } & A x \leqslant b, \\ & x_i \geqslant 0, i=1,2, \cdots, n, \\ & x_i \in \mathbb{Z}, i=1,2, \cdots, n, \end{array} \]
其中Z为所有的整数集合
例-仓库位置选取问题
