凸函数（Convex Function）

发表于 分类于

第三课：凸函数

凸函数的定义

定义1

对于一个函数\(f:\mathbb{R}^n\rightarrow\mathbb{R}\)，如果\(domf\)为凸集，且： \[ f(\theta x+(1-\theta)y)\le\theta f(x)+(1-\theta)f(y) \] 对所有的\(x,y\in domf,0\le\theta\le 1\)成立，则\(f\)为（下）凸函数

image-20230921125358565

连接凸函数的图像上任意两点的线段都在函数图像上方

  • \(f\)是凸函数，则\(-f\)是凹函数

  • 如果\(dom f\)是凸集，且 \[ f(\theta x+(1-\theta)y)<\theta f(x)+(1-\theta)f(y) \]

对所有的\(x,y\in domf,x\neq y,0<\theta <1\)成立，则\(f\)是严格凸函数

定义2

  • \(f\)是凸函数的充分必要条件为：\(\forall x,v\in domf,g(t)=f(x+tv)\)是凸函数

  • 证明

定义3（一阶条件）

  • 可微：如果\(dom f\)为开集，且函数的导数： \[ \nabla f(x)=(\frac{\partial f(x)}{\partial x_1},\frac{\partial f(x)}{\partial x_2},···,\frac{\partial f(x)}{\partial x_n}) \] 对所有定义域中的值都存在，则函数\(f\)可微

  • 一阶条件：对于可微函数\(f\)，如果\(domf\)为凸集，则\(f\)为凸函数当且仅当： \[ f(y)\ge f(x)+\nabla f(x)^T (y-x)\quad \text{for all }x,y\in domf \]

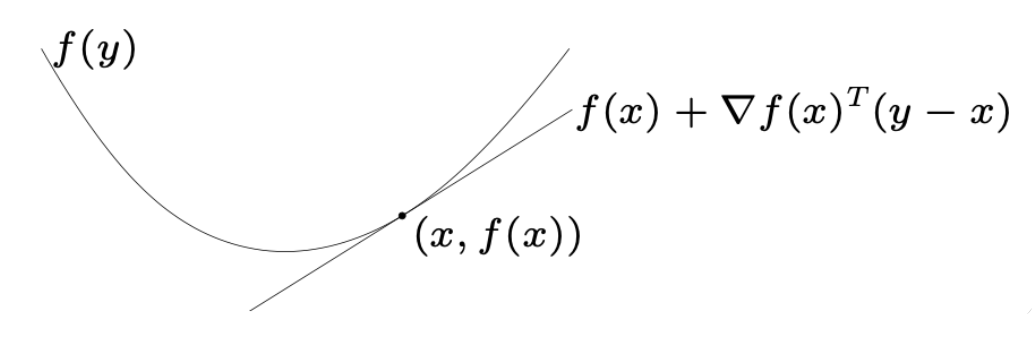
image-20230921125426877

意义：凸函数在局部的一阶泰勒展开是对函数值的低估

一阶条件的证明

  • =>

    f

  • <=

定义4（二阶条件）

  • 二阶可微：如果\(domf\)为开集，且函数的\(Hessian\)矩阵满足\(\nabla^2 f(x)\in S^n\) \[ \nabla^2 f(x)_{ij}=\frac{\partial^2 f(x)}{\partial x_i \partial x_j},i,j=1,...,. \] 对所有定义域中的值都存在，则函数\(f\)二阶可微

  • 二阶条件：对于二阶可微函数\(f\)，如果定义域为凸集

    • \(f\)为凸函数当且仅当： \[ \nabla^2 f(x)\succeq 0\quad \text{for all }x\in domf \]

    • 如果对所有定义域内的\(x\)满足\(\nabla^2 f(x)\succ 0\)，则\(f\)为严格凸函数

常见的凸函数

一维空间举例

image-20230921125640656

向量范数

image-20230921125652921

多维空间举例

多维向量\(R^n\)

  • 仿射函数：\(f(x)=a^Tx+b\)
  • 范数函数：\(\|x\|_p=(\sum_{i=1}^{n}|x_i|^p)^{\frac{1}{p}}\quad\text{for }p\ge1\)
  • 极大值函数：\(f(x)=\max\{x_1,...,x_n\},x\in R^m\)
  • \(L0\)范数：\(x\)中非零元素的个数

例：二次函数

  • 二次函数：\(f(x)=\frac{1}{2}x^TPx+q^Tx+r,P\in S^n\) \[ \nabla f(x)=Px+q,\quad\nabla^2f(x)=P \] 当P为半正定矩阵\((P\succeq 0)\)时为凸函数

  • 最小二乘目标函数：\(f(x)=\|Ax-b\|^2_2\) \[ \nabla f(x)=2A^T(Ax-b),\quad\nabla^2 f(x)=2A^TA \] 对任意的\(A\)都为凸函数

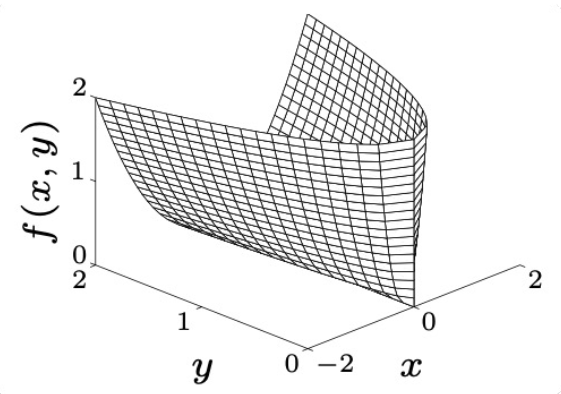
  • 二次函数比线性函数：\(f(x,y)=x^2/y\)对所有的\(y>0\)都为凸函数

image-20230921125739507

半正定矩阵的性质

矩阵A为行列式，则存在以下性质：

  • A的特征值均为负的。
  • 存在n阶实矩阵C，使\(A=C^TC.\)
  • A的行列式是负的

保持凸性的操作

验证⼀个函数是否是凸函数的方法

  1. 根据3种定义
  2. 验证函数是由多个相对简单的凸函数通过一些保持凸性的操作来得到

保持凸性的操作1：非负加权和

  • 命题：若\(f_1,...,f_m\)为凸函数，则\(f=\sum^m_{i=1}w_if_i\)为凸函数，\(w_i\ge0\)
  • 证明
    1. 定义域是否为凸集

保持凸性的操作2：仿射组合

  • 命题：若\(f\)为凸函数，则\(𝑓(𝐴𝑥+𝑏)\)为凸函数
  • 证明

保持凸性的操作3：最大化/极大化

最大化与极大化

  • \(\max\)：最大值

  • \(\sup\)：上确界

  • 命题：若\(f_1,...,f_m\)为凸函数，则\(f(x)=\max\{f_1(x),...,f_m(x)\}\)为凸函数

    • 证明：

  • 命题：若\(f(x,y)\)对所有\(y\in A\)为关于\(x\)的凸函数，则\(f(x)=\sup_{y\in A}f(x,y)\)为凸函数

保持凸性的操作4：标量函数的组合

对于函数\(g:R^n\to R^k\)与函数\(h:R^k\to R\)，函数组合为\(f(x)=h(g(x))\)

考虑\(n=k=1\)的情况

\(f\)为凸函数如果：\(\begin{cases}g是凸函数，h是凹函数，h递增\\g是凹函数，h是凸函数，h递减\end{cases}\) \[ f''(x)=h''(g(x)g'(x))^2+h'(g(x))g''(x). \]

例：

\(\exp g(x)当g是凸函数时为凸函数\)

\(1/g(x)当g是凹函数且为正时为凸函数\)

共轭函数（conjugate function）

函数\(f\)的共轭定义

\[ f^*(y)=\sup_{x\in domf}(y^Tx-f(x)) \]

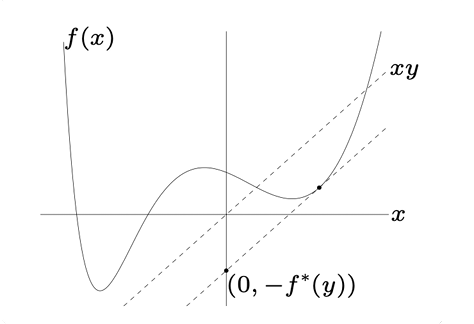
image-20230921170043534

性质：\(f^*(y)\)一定为凸函数